Tension
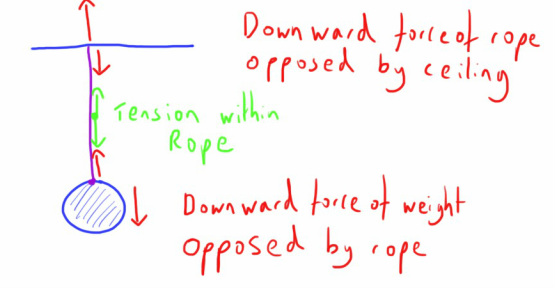
Tension is a specific form of force that is encountered in several areas of human physiology and so a review of it will prove useful.
Aspects such as surface tension and wall tension will crop up in respiratory and cardiovascular physiology in particular and I've found that understanding these concepts by looking at the basics first has really helped my understanding.
Aspects such as surface tension and wall tension will crop up in respiratory and cardiovascular physiology in particular and I've found that understanding these concepts by looking at the basics first has really helped my understanding.
What is Tension?
Other than the feeling you get prior to a big exam, tension is a physical concept relating to forces.
It can be considered as the opposite of a compression force; i.e. it is the resistance of a substance to external pulling force.
At a molecular level it can be viewed as the intermolecular attraction that prevents the molecules from pulling apart from each other.
It can be considered as the opposite of a compression force; i.e. it is the resistance of a substance to external pulling force.
At a molecular level it can be viewed as the intermolecular attraction that prevents the molecules from pulling apart from each other.
We never really encounter the classic tension in rope examples in human physiology, but as I mentioned above we do come across the concept of tension in a few certain areas.
As it is a force it is usually measured in Newtons and the force is parallel to the substance in question (the length of rope in the example above).
As it is a force it is usually measured in Newtons and the force is parallel to the substance in question (the length of rope in the example above).
Surface Tension
This is the tension force that exists on the surface of a liquid.
As with the concept of tension it is caused by the intermolecular attraction of molecules.
However, there are special characteristics that are noticed at the interface of a liquid with another substance.
This is classically seen and best described with the example of water as its strong intermolecular forces allow clear everyday examples of surface tension to be witnessed.
As with the concept of tension it is caused by the intermolecular attraction of molecules.
However, there are special characteristics that are noticed at the interface of a liquid with another substance.
This is classically seen and best described with the example of water as its strong intermolecular forces allow clear everyday examples of surface tension to be witnessed.
As we already know (from the chemistry section of this site...) water molecules exist as dipoles due to the strongly electronegative oxygen atom pulling the electrons in the covalent bonds towards it.
This slight polarity allows relatively strong intermolecular forces to exist, described as hydrogen bonds.
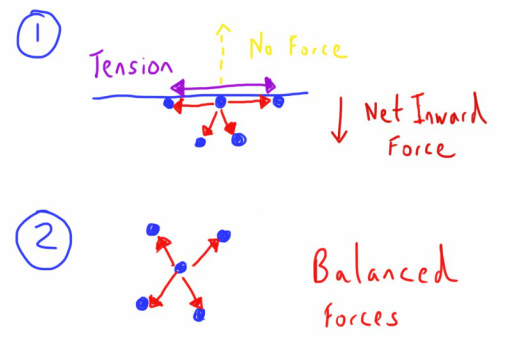
As we can see in the diagram below, in the middle of a volume of water (part 2), the force of these bonds is pulling on each molecule equally in all direction.
However, at the surface of the water (part 1) this is not possible and so the force of these intermolecular attractions will not be present in the direction away from the liquid surface.
This slight polarity allows relatively strong intermolecular forces to exist, described as hydrogen bonds.
As we can see in the diagram below, in the middle of a volume of water (part 2), the force of these bonds is pulling on each molecule equally in all direction.
However, at the surface of the water (part 1) this is not possible and so the force of these intermolecular attractions will not be present in the direction away from the liquid surface.
What does this mean? Well it means that there is an imbalance of forces which is inherently unstable.
As such the liquid will respond by minimising this imbalance, and the best way to minimise this imbalance is to minimise the surface area of the water and allow as many of the molecules to be in situation 2 above, rather than situation 1.
Geometrically, the shape with the smallest surface area to volume ratio is a sphere.
In the absence of other forces, this is the shape that a liquid will take.
The intermolecular forces of water are so strong that this can be seen clearly even in the presence of other strong forces (raindrops are good examples).
As such the liquid will respond by minimising this imbalance, and the best way to minimise this imbalance is to minimise the surface area of the water and allow as many of the molecules to be in situation 2 above, rather than situation 1.
Geometrically, the shape with the smallest surface area to volume ratio is a sphere.
In the absence of other forces, this is the shape that a liquid will take.
The intermolecular forces of water are so strong that this can be seen clearly even in the presence of other strong forces (raindrops are good examples).
The intermolecular forces that act between the surface molecules, pulling them in to this shape, result in surface tension.
LaPlace's Law and Wall Tension
So let's think about wall tension and physiology.
Unfortunately we're going to start with an equation which is LaPlace's Law.
Unfortunately we're going to start with an equation which is LaPlace's Law.
This equation gives us useful information about the relationship of pressure, wall tension and radius of a sphere (there is a very similar equation for cylinders which is applicable for blood vessels, the only difference being the absence of the 2 as part of the numerator - there is only one plane of tension compared with two planes in a sphere).
I initially found this equation a little bit of a challenge to get my head around, but a few examples and playing with the different components makes it clearer.
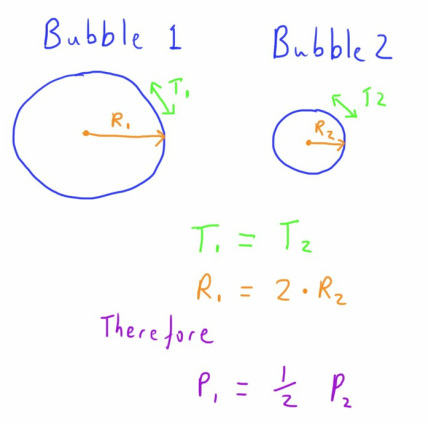
Picture 2 bubbles of different sizes in a tub of water.
They will each have the same tension in their walls (as it is the same intermolecular forces forming the wall) but with a smaller radius there will be a larger transmural pressure.
If these 2 bubbles come in to contact with each other the higher pressure in the smaller bubble will result it the air from the smaller bubble entering the larger one.
Picture 2 bubbles of different sizes in a tub of water.
They will each have the same tension in their walls (as it is the same intermolecular forces forming the wall) but with a smaller radius there will be a larger transmural pressure.
If these 2 bubbles come in to contact with each other the higher pressure in the smaller bubble will result it the air from the smaller bubble entering the larger one.
So this gives us an explanation as to why smaller bubbles are unstable, and have a tendency to join to form larger ones (something that is very noticeable when you become aware of it).
Why is this of any physiological interest?
Well alveoli in the lung are basically just small bubbles (very small bubbles in fact).
When we look at LaPlace's Law we can see that these bubbles are therefore going to be pretty unstable and have a tendency to collapse.
Indeed this would be the case if it wasn't for the surfactant produced by the alveoli cells to modulate the tension in the alveoli walls, thus preventing this from happening (check out the video on surfactant for more about this).
Well alveoli in the lung are basically just small bubbles (very small bubbles in fact).
When we look at LaPlace's Law we can see that these bubbles are therefore going to be pretty unstable and have a tendency to collapse.
Indeed this would be the case if it wasn't for the surfactant produced by the alveoli cells to modulate the tension in the alveoli walls, thus preventing this from happening (check out the video on surfactant for more about this).
LaPlace's Law Explained
Let's have a think about why LaPlace's Law works.
I find it easiest to have a think about the vectors at play in different walls.
If you remember right at the start we described how tension was the force parallel to the substance under tension (in this case the wall).
Knowing this we can have a think about the direction that this force is being applied.
I find it easiest to have a think about the vectors at play in different walls.
If you remember right at the start we described how tension was the force parallel to the substance under tension (in this case the wall).
Knowing this we can have a think about the direction that this force is being applied.
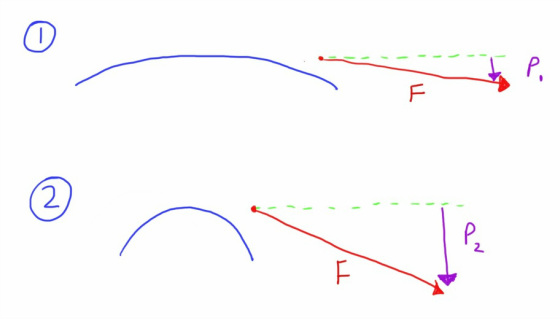
In the diagram above we have 2 different walls under the same degree of tension, as represented by the length of the force vector (F).
As the walls are curved this force will be distributed in different directions depending on the steepness of the curvature.
A steeper curve (as results from a smaller radius) allows a greater degree of force to be transmitted internally (P2 compared with P1).
Internally transmitted force will result in pressure.
As the walls are curved this force will be distributed in different directions depending on the steepness of the curvature.
A steeper curve (as results from a smaller radius) allows a greater degree of force to be transmitted internally (P2 compared with P1).
Internally transmitted force will result in pressure.
In Summary
Let's summarise LaPlace's Law into some useful nuggets.
- When the same tension exists in the wall of different spheres, as smaller sphere will have greater internal pressure.
- When the same pressure exists within different spheres, a larger sphere will require greater wall tension to contain the pressure.